최소신장트리(Minimum Spanning Tree)

📢  가중그래프

• 가중그래프(Weighted Graph) : 각 간선이 무게(weight)라 부르는 수치값을 가지는 그래프
• 무게가 될 수 있는 것들은 거리,비용,시간 등 다양하다.

가중그래프의 예시

 

📢  최소신장트리

• 신장 부그래프(Spanning Subgraph) : 그래프 G의 모든 정점들을 포함하는 부그래프
• 신장트리(Spanning Tree) : (자유)트리인 신장 부그래프
• 최소신장트리(MST, Minimum Spanning Tree) : 가중그래프의 총 간선 무게가 최소인 신장트리
• 응용분야
  
  👉 교통망, 통신망 등등

최소신장트리 예시 ( 파란색 경로가 추가될 경우 Cycle 생성됨 X )

• 최소신장트리 속성
  
  👉 1. 싸이클속성
  👉 2. 분할 속성
  
  이 두개의 속성은 알고리즘의 정확성 검증에 이용한다.

 

📢  싸이클 속성

f를 e로 대체하면 더 좋은 신장트리를 얻는다.

• 싸이클 속성
  
  👉 T를 가중그래프 G의 최소신장트리라 가정하자.
  👉 e를 T에 존재하지 않는 G의 간선으로, C를 e를 T에 추가하여 형성된 싸이클로 가정하자.
  👉 그러면 C의 모든 간선 f에 대해, weight(f) <= weight(e) 이다.
  
  
• 증명
  
  👉 모순법 : 만약 weight(f) > weight(e)라면, f를 e로 대체함으로써 무게가 더 작은 신장트리를 얻을 수 있기 때문

 

📢  분할 속성

• 분할 속성
  
  👉 G의 정점들을 두 개의 부분집합 U와 V로 분할한다고 하자.
  👉 e를 분할을 가로지르는 최소 무게의 간선이라고 하자.
  👉 간선 e를 포함하는 G의 최소신장트리가 반드리 존재한다.
  
  
• 증명
  
  👉 T를 G의 MST라 하자.
  👉 만약 T가 e를 포함하지 않는다면, e를 T에 추가하여 형성된 싸이클 C를 구성하는 간선들 가운데 분할을
  가로지르는 간선 f가 존재할 것이다.
  👉 싸이클 속성에 의해, weight(f) <= weight(e)
  👉 그러므로, weight(f) == weight(e)
  👉 f를 e로 대체하면 또 하나의 MST를 얻을 수 있다.

 

📢  최소신장트리 알고리즘

• 크게 3가지 알고리즘이 존재한다.
  
  👉 1. Prim-Jarnik 알고리즘 ( 많이 씀 )
  👉 2. Kruskal 알고리즘 ( 많이 씀 )
  👉 Baruvka 알고리즘 ( 1번 + 2번 느낌 )

 

📢  Prim-Jarnik 알고리즘

• 탐욕(Greedy) 알고리즘의 일종
• 대상 : 단순 연결 무방향 그래프
• 아이디어
  
  👉 임의의 정점 s를 택하여, s로부터 시작해서, 정점들을 (가상의)배낭에 넣어가며 배낭 안에서 MST T를 키워 나감
  👉 s는 T의 루트(root)가 될 것이다.
  👉 각 정점 v에 라벨 d(v)를 정의 = d(v)는 배낭 안에 정점과 배낭 밖 정점을 연결하는 간선의 weight
  👉 반복의 각 회전에서
  : 배낭 밖 정점들 가운데 최소 d(z) 라벨을 가진 정점 z를 배낭에 넣고, z에 인접한 정점들의 라벨을 갱신한다.

Alg PrimJarnikMST(G)
	input a simple connected weighted graph G with n vertexs and m edges
    output an MST T for G
    
for each v ∈ G.vertexs()
    d(v) <- ∞		// 여기서, d(v)는 각 정점들의 거리
    p(v) <- ∅		// 여기서, p(v)는 각 정점들의 MST로 이뤄지기위한 직계 부모 정점 정보

s <- a vertex of G
d(s) <- 0
Q <- a priority queue containing all the vertexs of G using d labels as keys

while(!(Q.isEmpty())	// 우선순위 큐를 비울 때까지 반복인데, 반복 작업은, 배낭(MST)에 정정을 하나씩 넓혀가는 것
    u <- Q.removeMin()	// 우선순위 큐에 들어가있는, 가장 거리 d 가 작은 정점 반환 u
    for each e ∈ G.incidentEdges(u)	// 정점 u에 부착된 간선 전부를 본다.
        z <- G.opposite(u,e)	// 정점 u와 이어진 간선 e를 통한 반대편 정점을 z라 한다.
        if((z ∈ Q) & (w(u,z) < d(z)))	// 정점 z가 우선순위 큐에 있는 것이고, 즉 아직 방문 안한 정점이고, 정점 u를 거쳐 정점 z로 가는 거리가, 아직 현재 정점 z거리보다 적으면
            d(z) <- w(u,z)		// 정점 z의 거리를 업데이트한다.
            p(z) <- e		// 그리고, 정점 z의 부모간선을 e로 업데이트한다.
            Q.replaceKey(z,w(u,z))	// 이렇게, 정점 z의 거리(d)가 우선순위가 바꼈을 수도 있으니, 우선순위큐 재배치를 진행한다.
            

 

• 추가설명
  
  👉 (가상의)배낭 밖의 정점들을 우선순위 큐에 저장 : 키(거리)-원소(정점정보)
  👉 각 정점 v에 세 개의 라벨을 저장한다.
  
  1. 거리(distance) : d(v)
  2. 위치자(locator) : 우선순위 큐에서의 v의 위치
  3. 부모(parent) : p(v), MST에서 v의 부모를 향한 간선

ㅌPrim-Jarnik 알고리즘 예시

• 알고리즘 분석
  
  👉 라벨 작업 : 점정 z의 거리, 부모, 위치자 라벨을 O(deg(z))시간 읽고 쓴다. 라벨을 읽고 쓰는데 O(1)시간 소요
  👉 우선순위 큐( 힙으로 구현할 경우 ) 작업
  
  1. 각 정점은 우선순위 큐에 한번 삽입되고 한번 삭제 : 삽입과 삭제에 각각 O(log(N))시간 소요
  2. 우선순위 큐 내의 정점 w의 키는 최대 deg(w)번 변경 : 각 키 변경에 O(log(N))시간 소요 (힙 이니깐)
  
  👉 그래프가 인접리스트 구조로 표현되어 있다면, Prim-Jarnik 알고리즘은 O((N+M)log(N))시간에 수행한다.
  👉 단순 연결그래프에서 N = O(M)이므로, 총 실행시간 : O(Mlog(N))

 

📢 Kruskal 알고리즘

• 탐욕(Greedy) 알고리즘
• 알고리즘을 위한 초기 작업
  
  👉 모든 정점을 각각의 독자적인 (실제의)배낭에 넣는다.
  👉 배낭 밖 간선들을 우선순위 큐에 저장한다. = 키(무게)-원소(간선)
  👉 비어 있는 MST T를 초기화
  
  
• 반복의 각 회전에서
  : 두 개의 다른 배낭 속에 양끝점을 가진 최소 무게의  간선을 MST T에 포함하고 두 배낭을 하나로 합친다.
• 반복이 완료되면
  : MST T를 포함하는 한 개의 배낭만 남게 될 것이다.

Alg KruskalMST(G)
	input a simple connected weighted graph G with n vertexs and m edges
    output an MST T for G

for each v ∈ G.vertexs()
    define a Sack(v) <- {v}		// Sack은 배낭을 의미, 이것은 실제 구현에서는 Parent(v)로 제어하면 편하다.

Q <- a priority queue containnig all the edges of G using weights as keys
T <- ∅

while(T has fewer than n - 1 edges)
   (u,v) <- Q.removeMin()
   if(Sack(u) ≠ Sack(v))
       Add edge (u,v) to T
       Merge Sack(u) and Sack(v)

return T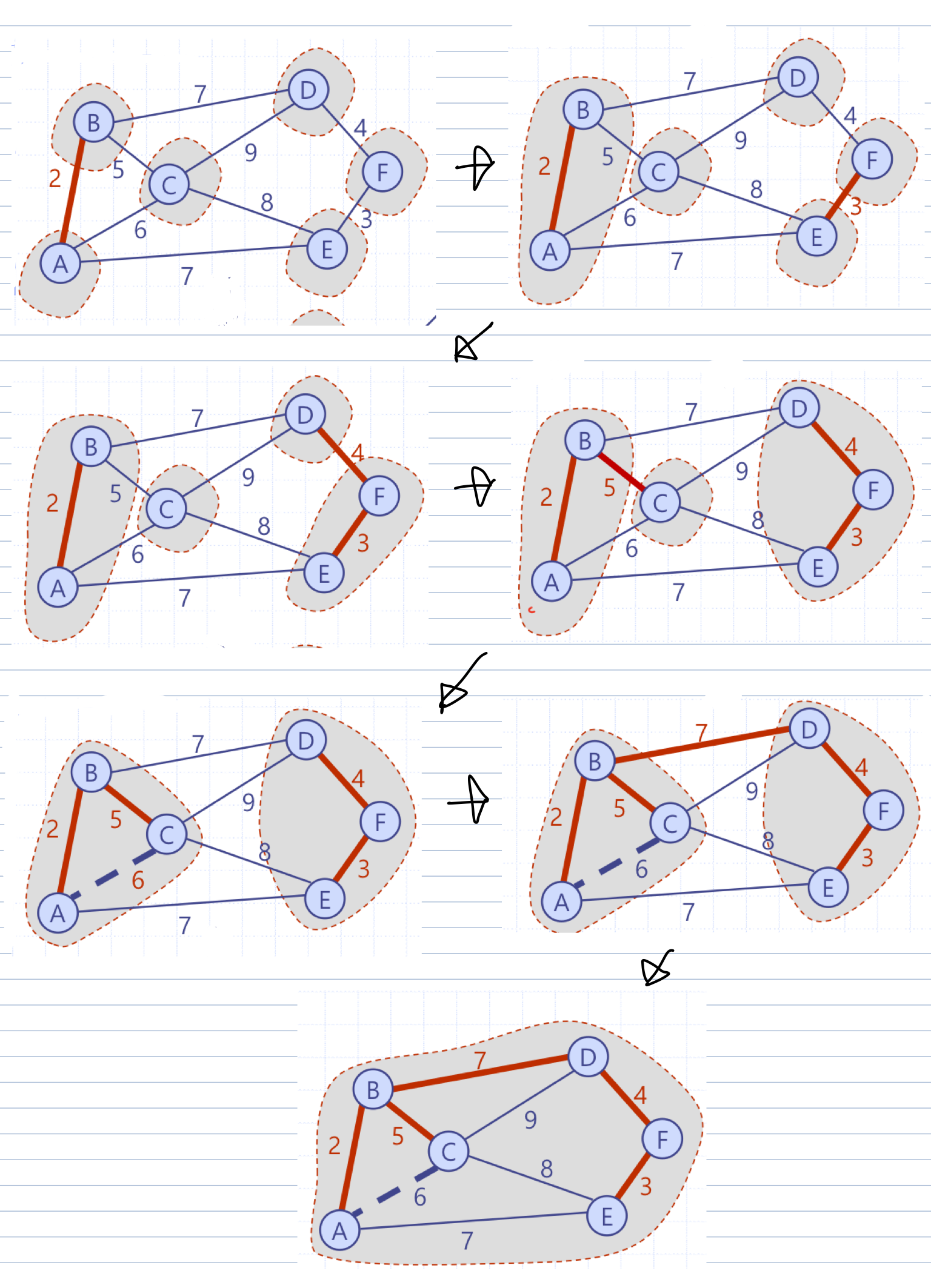

아Kruskal 알고리즘 예시

• 알고리즘 분석
  
  👉 우선순위 큐 초기화 작업
  
  힙을 사용하여 우선순위 큐 Q를 구현하면, 반복적인 삽입 방식에 의해서는 O(Mlog(M))시간에,
  상항식 힙 생성 방식에 의해서는 O(M) 시간에 Q 생성이 가능하다.
  
  👉 반복의 각 회전에서는
  
  최소 무게의 간선을 O(log(M))시간에  삭제 가능 = 여기서, G가 단순그래프이므로, O(log(M)) = O(log(N))
  각 배낭을 위한 분리집합을 리스트로 구현하면, find(u) ≠ find(v) 검사에 O(1) 시간 ( 또는 parent 배열을 이용 ! )
  두 개의 배낭 Sack(u), Sack(v)를 합치는데 O(min( |Sack(u)|, |Sack(v)| )) 시간 소요 ( 더 작은 배낭을 옮김 )
  
  👉 총 반복 회수 : (최악의 경우) M번
  👉 그러므로, Kruskal 알고리즘은 O((N + M)log(N)) 시간에 수행
  👉 G가 단순 연결그래프인 경우 N = O(M)이므로, 실행시간은 O(Mlog(N)) 이다.

 

📢  MST 알고리즘 비교

알고리즘	주요전략	수행시간	외부 데이터구조
Prim-Jarnik	탐욕	O(Mlog(N))	정점들을 저장하기 위한 우선순위 큐
Kruskal	탐욕	O(Mlog(N))	1. 간선들을 저장하기 위한 우선순위 큐 2. 배낭들을 구현하기 위한 분리집합(리스트로 구현가능) or 각 정점에 대해 부모정점(Parent배열)배열을 이용하는 방법