📢 이진탐색트리(Binary Search Tree)
-
내부노드에 (키,원소)쌍을 저장하며 다음의 성질을 만족하는 이진트리
성질
트리노드 u,v,w가 있을때, u와 w가 각각 v의 왼쪽과 오른쪽 부트리에 존재할 때 Key(u) < Key(v) < Key(w) 성립 -
전제 : 적정이진트리로 구현
[DS] 이진 트리 - binary tree (개념 및 이진 트리의 종류)
트리 Tree 는 원소들을 계층적으로 저장하는 비선형 non-linear 자료구조입니다. * 위 그림의 나무를 뒤집어 둔 것과 비슷하게 생겼습니다. 최상의 원소 루트 root를 제외한 각각의 원소는 하나의 부
sean-ma.tistory.com
-
이진탐색트리를 중위순회(Inorder Traversal)하면 키가 증가하는 순서로 방문한다.
[자료구조] 트리(Tree)의 개념 및 전위순회, 중위순회, 후위순회, 층별순회
안녕하세요! ㅋㅋ 자료구조는 아직 포스팅할 예정이 없었는데 매틀랩 자료를 올리려다 보니 트리에 대한 개...
blog.naver.com
-
이진탐색 트리 예

📢 이진탐색트리 탐색
-
Key를 찾기 위해, 루트에서 출발하는 하향 경로를 추적한다.
-
다음 방문할 노드는 Key와 현재 노드의 Key의 크기를 비교한 결과에 따라 결정한다.
- 외부노드(External Node, 리프노드(Leaf Node))에 다다르면, 찾는 Key가 발견되지 않은 것이다.

📢 이진탐색트리 삽입
-
우선 Key를 탐색한다.
-
Key가 현재 이진탐색트리에 존재하지 않을 경우 👉 탐색은 외부노드(w로 가정)에 도착
-
도착한 외부노드 w에 Key를 삽입한 후 👉 이 외부노드를 내부노드로 확장해줘야 한다.
-
여기서 외부노드 👉 Key값을 가지지 않은 트리의 말단에 위치한 노드
내부노드 👉 Key값을 가지고 있는 노드
Alg insertItem(K, E) // 이진탐색트리 삽입
input binary search tree T, Key K, element E
output none
w <- treeSearch(root(),K) // 일단, 이진탐색으로, K를 Key값으로하는 노드가 현재 있나 탐색
if(isInternal(w)) // 반환된 w노드가 내부노드 -> 이미 이진탐색트리 내에 존재한다는 것
return // 삽입 할 필요 X -> 종료
else // 외부노드인 경우
Set node w to (K, E) // w노드의 Key값을 K, 원소를 E로 적용하고
expandExternal(w) // ★ 이 w노드를 내부노드로 확장한다.
returnAlg expandExternal(z)
input external node z
output none
l <- getnode()
r <- getnode()
l.left <- Ø
l.right <- Ø
l.parent <- z
r.left <- Ø
r.right <- Ø
r.parent <- z
z.left <- l
z.right <- r
return
📢 이진탐색트리 삭제
-
크게 Case 1, Case 2로 나뉜다.
-
Case 1 👉 삭제할 Key를 가진 노드의 양쪽 자식 노드 중 하나가 외부노드일 경우
Case 2 👉 삭제할 Key를 가진 노드의 양쪽 자식 노드 둘 다 내부노드일 경우 ★
📌 이진탐색트리 삭제 ( Case 1. 삭제할 노드 양쪽 자식노드 중 하나가 외부노드인 경우 )
-
삭제할 노드의 양쪽 자식 노드 중 하나가 외부노드일 경우이다.
-
우선 삭제할 Key를 탐색
-
Key가 트리에 존재할 경우, 탐색은 Key를 저장하고 있는 노드(w라 가정)에 도착
-
노드 w의 자식 중 하나가 외부노드(z라 가정)라면, 노드 w의 축소과정을 통해, w, z를 트리로부터 삭제한다.
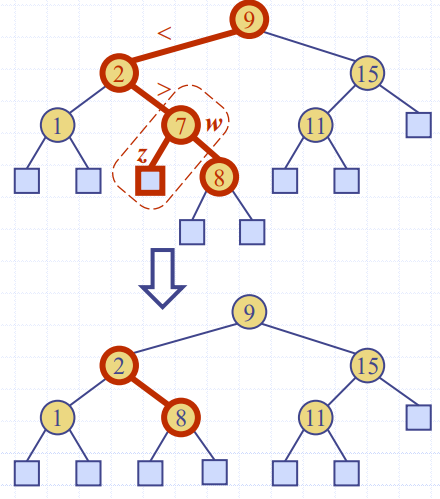
📌 이진탐색트리 삭제 ( Case.2 삭제할 노드의 양쪽 자식노드가 둘 다 내부노드 일 경우 ) ★
-
삭제할 노드의 양쪽 자식노드 둘 다 내부노드일 경우이다. ( 이 때 삭제할 노드는 w라 가정 )
-
1. 트리 T에 대해 w의 중위순회 계승자 y와 그 자식노드 z를 찾아낸다.
-
노드 y는 우선 w의 오른쪽 자식으로 이동한 후, 거기서부터 왼쪽 자식들만을 끝까지 따라 내려가면 도달하게 되는 마지막 내부노드이며, 노드 z는 y의 왼쪽 자식인 외부노드
-
y는 T를 중위순회할 경우, 노드 w바로 다음에 방문하게 되는 내부노드이므로, w의 중위순회 계승자(Inorder successor)라 불린다.
-
따라서, y는 w의 오른쪽 부트리 내 노드 중 가장 왼쪽으로 돌출된 내부노드이다.
-
-
2. y의 내용을 w에 복사
-
3. reduceExternal(z) 작업을 사용해서 노드 y와 z를 삭제

Alg removeElement(K)
input binary search tree T, Key K
output element with Key K
W <- treeSearch(root(),K)
// Key K를 가지는 T내에 찾은 w노드가 외부노드인 경우
if(isExternal(W))
return NoSuchKey
// Key K를 가지는 T내에 찾은 W노드가 외부노드인 경우
e <- element(W)
z <- leftChild(W)
if(!(isExternal(z))
z <- rightChild(W)
if(isExternal(z)) // Case 1. 삭제할 W노드의, 양쪽 자식노드 중 하나가 외부노드인 경우
reduceExternal(z)
else // Case 2. 삭제할 W노드의, 양쪽 자식노드 둘 다 내부노드인 경우 ★
y <- inOrderSucc(W) // W의 중위순회계승자( 즉, W노드의 Key값 바로 다음으로 큰, Key값을 가진 노드 ), y
z <- leftChild(y) // 중위순회계승자 y노드의 왼쪽 자식노드가 z
Set node W to (Key(y),element(y)) // 삭제한다는 개념으로, 삭제할 W노드의 key값과 element값을 y의 Key,element로 변경
reduceExternal(z) // y에 대해, 내부노드 축소과정
return e
📢 이진탐색트리의 성능
-
높이 h의 이진탐색트리를 사용하여 구현된 N 항목의 사전을 가정해보자.
-
O(N) 공간을 사용한다.
-
탐색,삽입,삭제 작업 모두 O(h)시간에 수행
-
높이 h는
1. 최악의 경우 👉 O(N)2. 최선의 경우 👉 O(log(N))

📢 참고
-
동일한 키 집단으로 생성된 이진탐색트리에서, 삽입 순서와는 상관없이 항상 동일한 이진탐색트리가 생성된다 ?👉 NO !!
- 간단한 예로 확인가능 👉 [ 9,5,12,7,13 ] 순서와 [ 9,7,12,5,13 ] 순서로 생성되는 이진탐색트리의 모양은 다르다.
'Algorithm Theory' 카테고리의 다른 글
| 그래프(Graph) (0) | 2020.12.13 |
|---|---|
| 해시테이블(Hash Table) (0) | 2020.12.13 |
| 사전(Dictionary) (0) | 2020.12.12 |
| 힙과 힙정렬 ( Heap & Heap Sort ) (0) | 2020.09.26 |
| 우선순위 큐(Priority queue) (0) | 2020.09.24 |