📢 방향그래프
- 방향그래프(Digraph) : 모든 간선이 방향간선인 그래프
📢 방향그래프 속성
- 모든 간선이 한 방향으로 진행하는 그래프 G = (V,E)에서
👉 간선(a,b)는 a -> b 로는 가지만, b -> a 로는 가지 않는다. - 그래프 G가 단순하다면 ( 즉, 병렬간선이나, 루프가 없으면 )
👉 M <= N(N-1) 이다. ( 무방향그래프에선 M <= (N(N-1)/2 였다. )
( 여기서 M = 간선 수, N = 정점 수 이다. ) - 진입간선들(in-edges)과 진출간선들(out-edges)을 각각 별도의 인접리스트로 보관한다면, 진입간선들의 집합과
진출간선들의 집합을 각각의 크기에 비례한 시간에 조사 가능하다.
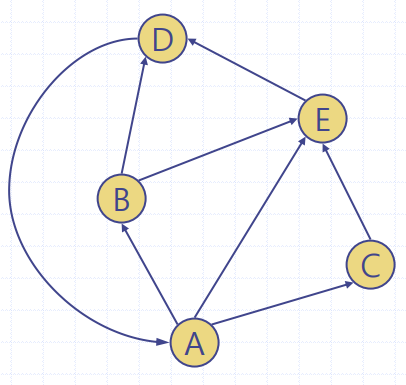

📢 방향 DFS
- 간선들을 주어진 방향만을 따라 순회하도록 하면, DFS 및 BFS 순회 알고리즘들을 방향그래프에 특화 가능하다.
- 방향 DFS 알고리즘에서 네 종류의 간선이 발생한다.
👉 트리간선(tree edges) : 트리에서, DFS경로에 해당하는 간선
👉 후향간선(back edges) : 트리에서 나의 조상방향으로 그려질 간선
👉 전향간선(forward edges) : 트리에서 나의 자식이 아닌, 더 아래 자식 정점의 경우 그려질 간선
👉 교차간선(cross edges) : 같은 레벨이나 하위레벨 정점끼리의 연결 간선 - 정점 s에서 출발하는 방향 DFS 👉 s로부터 도달 가능한 정점들을 결정한다.


- 도달 가능성이란 ?
👉 방향그래프 G의 두 정점 v와 u에 대해, 만약 G에 v에서 u로의 방향 경로가 존재한다면, "v는 u에 도달한다" 또는 "u는 v로부터 도달 가능하다" 를 의미한다.
👉 s를 루트로 하는 DFS 트리 : s로부터 방향경로를 통해 도달 가능한 정점들을 표시한 것

📢 강연결성
- 방향그래프 G의 어느 두 정점 u와 v에 대해서나 u는 v에 도달하며 v는 u에 도달하면
👉 G를 강연결(strongly connected)이라고 말한다. 즉, 어느 정점에서든지 다른 모든 정점에 도달 가능하다.

- 강연결 검사 알고리즘
👉 1. 그래프 G의 임의의 정점 v를 선택한다.
👉 2. 그래프 G의 v로부터 DFS를 수행한다. ( 방문되지 않은 정점 w가 있다면, False를 반환한다. )
👉 3. 그래프 G의 간선들을 모두 역행시킨 그래프 G` 를 얻는다.
👉 4. G`의 v로부터 DFS를 수행한다. ( 방문되지 않은 정점 w가 있다면, False를 반환. 그렇지 않으면, True 반환)
실행시간 = O(N + M)

- 강연결요소
👉 방향그래프서 각 정점으로 다른 모든 정점으로 도달할 수 있는 최대의 부 그래프
👉 DFS를 사용하여 O(N + M)시간에 계산 가능하다.

📢 이행적폐쇄
- 주어진 방향그래프 G에 대해, 그래프 G의 이행적폐쇄(Transitive Closure)는 다음을 만족하는 방향그래프 G*
👉 G* 는 G와 동일한 정점들로 구성
👉 G에 u로부터 v ≠ u 로의 방향경로가 존재한다면, G*에 u로부터 v로의 방향간선이 존재한다.
👉 더 쉽게, 수학적으로, "A -> B , B -> C 이면, A -> C" 를 의미하는 것 - 이행적폐쇄는 방향그래프에 관한 도달 가능성 정보를 제공한다.

- 이행적폐쇄 계산
👉 각 정점에서 출발하여 DFS를 수행할 수 있다.
실행시간 : O(N(N + M))) 👉 N개의 각 정점의 대해 * DFS - 대안으로, 동적프로그래밍(DP, Dynamic Programming)을 사용할 수 있다.
👉 Floyed-Warshall 알고리즘 : 위에서 설명한, "A -> B , B -> C 이면, A -> C"
📢 Floyed-Warshall 이행적폐쇄
- 정점들을 1,2,....n으로 번호를 매긴다.
- 1,2,....,k로 번호 매겨진 정점들만 경유 정점으로 사용하는 경로들을 고려해본다.

Alg Floyed-Warshall(G)
input a digraph G with n vertexs
output transitive closure G* of G
Let V(1),V(2),...,V(n) be an arbitrary numbering of the vertexs of G
G(0) <- G
for k <- 1 to n // Stopover vertex
G(k) <- G(k-1)
for i <- 1 to n, i ≠ k // start vertex
for j <- 1 to n, j ≠ i,k // end vertex
if(G(k-1).areAdjacent(V(i),V(k) & G(k-1).areAdjacent(V(k),V(j))
if(!(G(k).areAdjacent(V(i),V(j))
G(k).insertDirectedEdge(V(i),V(j),k)
return G(n)- Floyed-Warshall 알고리즘은 G의 정점들을 V(1),....,V(n)으로 번호 매긴 후, 방향그래프 G(0),....,G(n)을 잇달아 계산
👉 G(0) = G
👉 G에 { V(1),....V(k) } 집합 내의 경유정점을 사용하는 V(i)에서 V(j)로의 방향경로가 존재하면 G(k)에 방향간선
(V(i), V(j))를 삽입 - k 단계에서, 방향그래프 G(k-1)로부터 G(k)를 계산
- 마지막에 G(n) = G*를 얻음
- 실행시간 : O(n^3)
👉 전제 : 인접한지 알아보는 areAdjacent( )가 O(1)시간에 수행 ( 즉, 인접행렬 버젼일 경우 )

📢 방향 비싸이클 그래프
- 방향 비싸이클 그래프(DAG, Directed Acyclic Graph) : 방향싸이클이 존재하지 않는 방향그래프
- 예시
👉 클래스 간 상속 또는 인터페이스
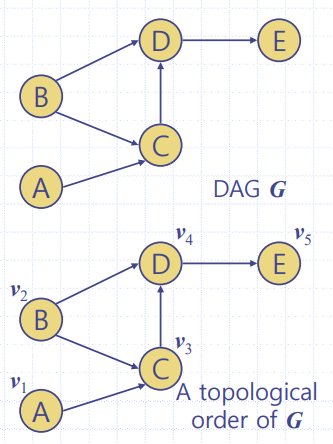
👉 교과 간의 선수 관계 등등 - 방향그래프의 위상순서(Topological Order)
👉 모든 i < j인 간선 (V(i),V(j))에 대해 정점들을 번호로 나열한 것이다.
👉 예시) 작업스케쥴링 방향그래프에서 위상순서는 작업들의 우선 d 만족하는 작업 순서
결론 : 방향그래프가 DAG 이면 👉 위상순서를 가지며, 그 역도 참이다.
📢 위상정렬(Topological Sort)
- 위상 정렬(Topological Sort) : DAG로부터 위상순서를 얻는 절차
- 알고리즘
👉 1. topologicalSort : 정점의 진입차수(in-degree)를 이용한 방법
👉 2. topologicalSortDFS : DFS의 특화된 방법 - 1. topologicalSort : 정점의 진입차수(in-degree)를 이용한 방법
Alg topologicalSort(G)
input a digraph G with n vertexs
output a topological ordering V(1),...,V(n) of G,
or an indication that G has a directed cycle
Q <- empty queue
for each u ∈ G.vertexs()
in(u) <- inDegree(u)
if(in(u) == 0)
Q.enqueue(u)
i <- 1 // topological number
while(!(Q.isEmpty())
u <- Q.dequeue()
Label u with topological number i
i <- i + 1
for each e ∈ G.outIncidentEdges(u)
w <- G.opposite(u,e)
in(w) <- in(w) - 1
if(in(w) == 0)
Q.enqueue(w)
if(i <= n) // i = n + 1, for DAG
write("G has a directed cycle) // DAG가 아님을 알리는 메시지
return
// 각 정점에 새로운 라벨을 정의 => 현재 진입차수(inCount) : in(v) => 정점 v의 현재의 진입차수 계산
- 2. topologicalSortDFS : DFS를 활용한 위상정렬
Alg topologicalSortDFS(G)
input DAG G
output topological ordering of G
n <- G.numVertexs()
for each u ∈ G.vertexs()
l(u) <- Fresh
for each v ∈ G.vertexs()
if(l(v) == Fresh)
rTopologicalSortDFS(G,v)
=========================================
Alg rTopologicalSortDFS(G,v) // 재귀적 DFS를 활용한 위상정렬
input graph G, and a start vertex v of G
output labeling of the vertexs of G
in the connected component of v
l(v) <- Visited
for each e ∈ G.outIncidentEdges(v)
w <- opposite(v,e)
if(l(w) == Fresh) // 간선 e는 tree 간선
rTopologicalSortDFS(G,w)
Label v with topological number n
n <- n - 1 // 전역 변수로 제어할 것이다.
- 위상 정렬 알고리즘 비교
1. topologicalSort : 정점의 진입차수를 이용한 버젼
👉 O(N + M) 시간과 O(N) 공간 소요
👉 그래프 G가 DAG라면 위상순서를 계산
👉 그래프 G에 방향싸이클이 존재할 경우, 일부 정점의 순위를 매기지 않은 채로 "정지"
2. topologicalSortDFS : DFS 활용한 버젼
👉 O(N + M) 시간과 O(N) 공간 소요
👉 그래프 G가 DAG라면 G의 위상순서를 계산
👉 그래프 G에 방향싸이클이 존재할 경우, 허위의 위상순서를 계산 = 방향싸이클을 발견하도록 수정 가능함 !!
728x90
반응형
'Algorithm Theory' 카테고리의 다른 글
| 최소신장트리(Minimum Spanning Tree) (0) | 2020.12.15 |
|---|---|
| 동적프로그래밍(Dynamic Programming) (0) | 2020.12.14 |
| 그래프 순회(Graph Traversal) (0) | 2020.12.14 |
| 그래프(Graph) (0) | 2020.12.13 |
| 해시테이블(Hash Table) (0) | 2020.12.13 |