📢 그래프(Graph)
- 그래프(Graph) : (V,E)쌍, 여기서 V,E는 각각
👉 V : 정점(Vertex)이라 불리는 노드의 집합
👉 E : 간선(Edge)이라 불리는 정점쌍들의 집합 - 정점(V)과 간선(E)은 원소, 즉 정보를 저장한다.
📢 간선에 따른 그래프 유형
- 방향간선(Directed edgd)
👉 정점들의 순서쌍 (u,v)
👉 u : 시점(Origin)
👉 v : 종점(Destination) - 방향그래프(Directed Graph)
👉 모든 간선이 방향간선인 그래프

- 무방향간선(Undirected edge)
👉 정점들의 무순쌍 (u,v) - 무방향그래프(Undirected Graph)
👉 무방향간선으로 이루어진 그래프

- 그래프 응용분야
👉 교통망 : 고속도로망, 항공노선망
👉 컴퓨터 네트워크 : LAN(Local Area Network), 인터넷, 웹
👉 데이터베이스 : ER-Dirgram
👉 그 외에도, 아주 많은 분야에서 그래프 응용분야가 많다.
📢 그래프 용어정리

- 간선의 끝점(end Vertex, endpoint)
👉 정점 U와 V는 a의 양끝점 - 정점의 부착(Incident)간선
👉 a,d,b는 V에 부착한다. - 정점의 인접(Adjacent)정점
👉 U와 V는 인접하다. - 정점의 차수(Degree)
👉 X의 차수는 5다. - 병렬 간선(Parallel edges)
👉 h와 i는 병렬 간선 - 루프(Loop 또는 self-loop)
👉 j는 루프다.
- 경로(Path)
👉 정점과 간선의 교대열
👉 정점으로 시작하여 정점으로 끝난다.
👉 각 간선은 그 양끝점으로 시작하고 끝난다. - 단순경로(Simple path)
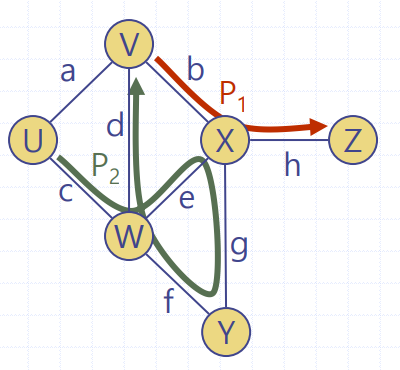
👉 모든 정점과 간선이 유일한 경로 - 예시
👉 P1 = (V,b,X,h,Z)는 단순경로 ( 위 그래프에서 경로 )
👉 P2 = (U,c,W,e,X,g,Y,f,W,d,V)는 비단순경로 ( 위 그래프에서 경로 )
- 싸이클(Cycle)
👉 정점과 간선이 교대 원형
👉 각 간선은 그 양끝점으로 시작하고 끝난다. - 단순싸이클(Simple Cycle)
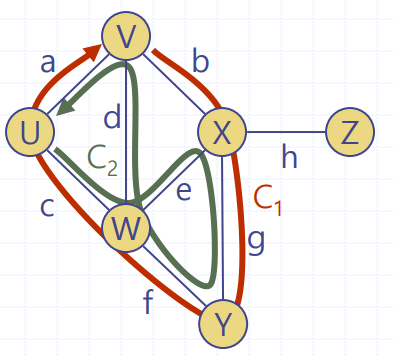
👉 모든 정점과 간선이 유일한 싸이클 - 예시
👉 C1 = (V,b,X,g,Y,f,W,c,U,a)는 단순싸이클 ( 위 그래프에서 경로 )
👉 C2 = (U,c,W,e,X,g,Y,f,W,d,V,a)는 비단순싸이클 ( 위 그래프에서 경로 )
📢 그래프 속성
- n = 정점 수, m = 간선 수, deg(v) = 정점 v의 차수 일때,
- 속성 1
👉 어떤 그래프의 차수(Degree) 합 = 2m ( m = 간선(edge)의 수 ) - 속성 2
👉 루프와 병렬 간선이 없는 무방향그래프에서, m <= (n(n-1) )/2)
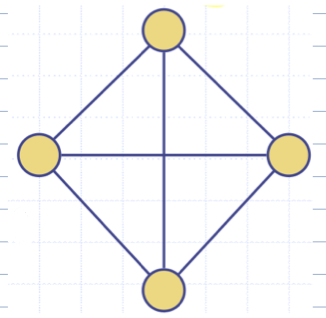
- 위와 같은 그래프가 있을 경우 ( n = 4, m = 6, deg(v) = 3 )
👉 최대 6 <= (4(4-1)/2) 가 성립한다.
📢 부그래프(Sub Graph)
- 그래프 G = (V,E)의, 부그래프(Sub Graph)는 다음 정점과 간선으로 구성된 그래프다.
👉 정점 : V의 부분집합
👉 간선 : E의 부분집합 - 그래프 G = (V,E)의, 신장부그래프(Spanning Subgraph)는 다음 정점과 간선으로 구성된 그래프다.
👉 정점 : V
👉 간선 : E의 부분집합


📢 연결성
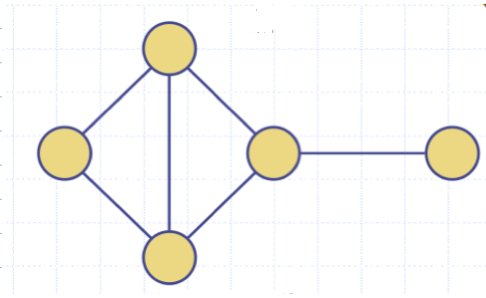
- 모든 정점쌍에 대해 경로가 존재하면, "그래프가 연결(Connected)되었다."라고 말한다.
- 그래프 G의 연결요소(Connected Component) : G의 최대 연결 부그래프

📢 밀집도
- 그래프 알고리즘의 선택은 종종 간선의 밀집도에 따라 좌우된다.
- 예로들어, 주어진 그래프 G에 대해, 알고리즘 A,B가 동일한 문제를 각각 O(NM)시간과 O(N^2)시간에 해결할 경우
👉 G가 희소하다면, 알고리즘 A가 B보다 빠르다.
👉 G가 밀집하다면, 알고리즘 B가 A보다 빠르다.


📢 싸이클
- 자유트리(Free Tree), 또는 트리 : 다음 조건을 만족하는 무방향그래프 T
👉 T는 연결되어있다.
👉 T에 싸이클이 존재하지 않는다.
❗❗ 자료구조의 "트리(Tree)"랑은 다른 개념이다. - 숲(Forest) : 싸이클이 없는 무방향그래프
- 숲의 연결요소는 트리"들"이다.

📢 신장
- 연결그래프의 신장트리(Spanning Tree) : 신장 부그래프 가운데 트리인 것
- 신장트리는 그래프가 트리가 아닌 한(즉, 싸이클이 존재하지 않는 한), 유일하지 않다.
- 신장트리는 통신망 설계에 응용한다.
- 그래프의 신장숲(Spanning Forest) : 신장 부그래프 가운데 숲인 것


📢 그래프 구현
- 그래프 구현에는 크게 3가지 구조로 가능하다.
👉 간선리스트(edge list)구조
👉 인접리스트(adjacency list)구조
👉 인접행렬(adjacency matrix)구조 - 인접리스트 구조는
👉 연결리스트를 이용한 구현
👉 배열을 이용한 구현

- 인접행렬 구조는
👉 연결리스트를 이용한 구현
👉 배열을 이용한 구현
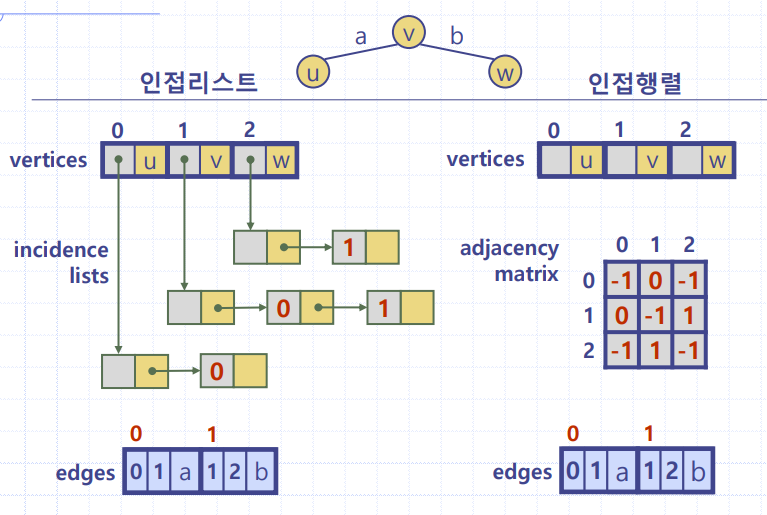
📢 인접행렬(Adjacency Matrix)
- N X N 행렬로 표현
- 무향 그래프의 경우
👉 원소(i,j) = 1 : 정점 i와 정점 j 사이에 간선이 있다.
👉 원소(i,j) = 0 : 정점 i와 정점 j 사이에 간선이 없다.

- 유향 그래프의 경우
👉 원소(i,j)는 정점 i 로부터 정점 j 로 연결되는 간선이 있는지를 나타낸다.

- 가중치 있는 그래프의 경우
👉 원소(i,j)는 1 대신에 가중치를 가진다.


📢 인접리스트(Adjacency List)
- N 개의 연결 리스트로 표현
👉 i 번째 리스트는 정점 i 에 인접한 정점들을 리스트로 연결해 놓은 것 - 가중치 있는 그래프의 경우
👉 리스트는 가중치도 보관한다.


📢 그래프 성능 & 특징
- 점근적 성능 비교
| N 정점과 M 간선 병렬 간선 없음 루프 없음 |
간선리스트 | 인접리스트 | 인접행렬 |
| 공간 | N + M | N + M | N^2 |
| incidentEdges(v) | M | deg(v) | N |
| adjacentVertexs(v) | M | deg(v) | N |
| areAdjacent(v,u) | M | min(deg(v),deg(u)) | 1 |
| insertVertex(o) | 1 | 1 | N |
| insertEdge(v,w,o) | 1 | 1 | 1 |
| removeVertex(v) | M | deg(v) | N |
| removeEdge(e) | 1 | 1 | 1 |
- 그래프 상세 구현 비교
| 인접리스트 | 인접행렬 | ||
| 연결리스트 | 정점리스트 간선리스트 |
동적메모리 노드의 연결리스트 | |
| 정점,간선 | 동적메모리 노드 | ||
| 인접 정보 | 포인터의 연결리스트 | 2D 포인터 배열 | |
| 장점 | 동적 그래프에 사용 시 유리 | ||
| 단점 | 다수의 포인터 사용으로 복잡 | ||
| 배열 | 정점리스트 간선리스트 |
구조체 배열 | |
| 정점,간선 | 구조체 | ||
| 인접 정보 | 첨자의 연결리스트 | 2D 첨자 배열 | |
| 장점 | 다수의 포인터를 첨자로 대체하여 단순 | ||
| 단점 | 동적 그래프에 사용 시 불리 | ||
📢 그래프 구현 ADT
- 단순한화한 무방향그래프 ADT 구현
👉 Integer deg(v) : 정점 v의 차수를 반환
👉 Integer opposite(v,e) : 정점 v와 간선 e에 대한 반대쪽 끝점을 반환
👉 Boolean areAdjcent(v,u) : 정점 v와 u가 인접한지 여부를 반환
👉 Iterator adjacentVertex(v) : 정점 v의 인접정점을 모두 반환
👉 Iterator incidentEdge(v) : 정점 v의 부착간선을 모두 반환 - A. 그래프가 인접리스트 구조로 표현된다.
- B. 그래프가 인접행렬 구조로 표현된다.
- 전제
👉 인접행렬 구조에서 인접행렬은 배열 A에 저장됬다.
👉 index(v) 함수 사용 가능 : 인접행렬에서 정점 v에 대응하는 배열첨자를 반환
차수 메소드( deg(v) )
Alg deg(v) // 인접리스트 버전
input vertex v
output integer
c <- 0
e <- (v.incidentEdge).next
while(e != ∅)
c <- c + 1
e <- e.next
return c
// Total = O(deg(v))
======================================
Alg dev(v) // 인접행렬 버전
input adjacency matrix A, vertex v
output integer
c <- 0
vi <- index(v)
for j <- 0 to n-1
if(A[vi,j] != ∅)
c <- c + 1
return c
// Total = O(n)나의 상대방 정점 반환 메소드( opposite(v,e) )
Alg opposite(v,e) // 인접리스트 버전
input vertex v, edge e
output vertex
u,w <- e.endpoints
if(v == u)
return w
else
return u
// Total = O(1)
==========================
Alg opposite(v,e) // 인접행렬 버전
input adjacency matrix A, vertex v, edge e
output vertex
u,w <- e.endpoints
if(v == u)
return w
else
return u
// Total = O(1)정점 v,w가 인접한지 확인 메소드( areAdjacent(v,w) )
Alg areAdjacent(v,w) // 인접리스트 버전
input vertex v,w
output boolean
if(deg(v) < deg(w))
m <- v
else
m <- w
e <- (m.incidentEdges).next
while(e != ∅)
a,b <- e.endpoints
if((v == a) && (w == b) || (v == b) && (w == a))
return True
e <- e.next
return False
// Total = O(min(deg(v),deg(w)))
=====================================================
Alg areAdjacent(v,w) // 인접행렬 버전
input adjacency matrix A, vertex v,w
output integer
return A[index(v),index(w)] != ∅
// Total = O(1)나의 인접한 정점 반환 메소드( adjacentVertex(v) )
Alg adjacentVertex(v) // 인접리스트 버전
input vertex v
output set of vertex objects
L <- empty list
e <- (v.incidentEdges).next
while(e != ∅)
L.addLast(opposite(v,e))
e <- e.next
return L.element()
// Total = O(deg(v)) // 자기랑 연결된 간선만 조사하면 되니깐
===================================
Alg adjacentVertex(v) // 인접행렬 버젼
input adjacency matrix A, vertex v
output set of vertex objects
L <- empty list
vi <- index(v)
for j <- 0 to n - 1
if(A[vi,j] != ∅)
L.addLast(opposite(v,A[vi,j]))
return L.element()
// Total = O(n) // 나를 제외한 모든 정점에 대해, 연결되어 있는지 하나씩 조사해야되니깐나의 부착간선 반환 메소드( incidentEdges(v) )
Alg incidentEdges(v) // 인접리스트 버젼
input vertex v
output set of edge objects
L <- empty list
e <- (v.incidentEdges).next
while(e != ∅)
L.addLast(e)
e <- e.next
return L.element()
// Total = O(deg(v)) // 나한테 부착된 연결리스트만 확인하면 되니깐
=================================
Alg incidentEdges(v) // 인접행렬 버젼
input adjacency matrix A, vertex v
output set of edge objects
L <- empty list
vi <- index(v)
for j <- 0 to n - 1
if(A[vi,j] != ∅)
L.addLast(A[vi,j])
return L.elements()
// Total = O(n) // 나를 제외한 모든 정점에 대해 부착됬는지 확인해야되니깐
📢 번외
- 그래프 구현 방식 선택 : 다음 각 경우에 인접리스트 구조와 인접행렬 구조 둘 중 어느 것을 사용하겠는가 ?
👉 a. 그래프가 10,000개의 정점과 20,000개의 간선을 가지며, 가능한 최소한의 공간 사용이 중요
👉 b. 그래프가 10,000개의 정점과 20,000,000개의 간선을 가지며 가능한 최소한의 공간 사용이 중요
👉 c. 얼마의 공간을 사용하든, areAdjacent 질의에 가능한 빨리 답해야 할 경우 - 해결책
👉 a. 인접리스트 구조가 유리 = 실상 인접행렬 구조를 쓴다면 많은 공간을 낭비한다. 왜냐면 20,000개의 간선만이 존재하는데도 100,000,000개의 간선에 대한 공간을 할당하기때문 ( M <= (N(N-1)/2 )
👉 b. 일반적으로, 이 경우에는 양쪽 구조 모두가 적합 = areAdjacent 작업은 인접행렬 구조가 유리, insertVertex와 removeVertex 작업에서는 인접리스트 구조가 유리
👉 c. 인접행렬 구조가 유리 = 이유는, 이 구조가 areAdjacent작업을 정점이나 간선의 개수에 관계없이 O(1)시간에 지원하기 때문이다. - O(log M) == O(log N)인 이유 ( M = 간선 수, N = 정점 수 )
👉 G를 N 개의 정점과 M 개의 간선으로 이뤄진 단순 연결그래프라 가정하자.
👉 M <= N(N-1)/2 이며, 이는 O(N^2)이다.
👉 따라서, O(log M) == O(log N^2) == O(2log N) == O(log N) 이다.
728x90
반응형
'Algorithm Theory' 카테고리의 다른 글
| 방향 그래프(Directed graph) (0) | 2020.12.14 |
|---|---|
| 그래프 순회(Graph Traversal) (0) | 2020.12.14 |
| 해시테이블(Hash Table) (0) | 2020.12.13 |
| 이진탐색트리(Binary Search Tree) (0) | 2020.12.12 |
| 사전(Dictionary) (0) | 2020.12.12 |